Histoire d'être plus rigolo, je vais changer de sujet, et on va parler ROF.
Imaginons le cas d'une HMG qui va tirer à 6 FP, 0 DRM. Et soyons suffisamment sympathiques pour oublier un instant qu'un DR 12 la cassera.
Le tir d'une telle arme dirigée sur une unité dont le moral est 7 (DRM 0) ne provoquera aucun Pin, Break, K/ ou KIA dans 663 cas sur 36^2 (deux lancers de dés consécutifs, un pour l'IFT l'autre pour le MC ou le PTC). On dira donc que son taux de No Impact est de 663/36^2 soit environ 51 %.
Nous savons aussi que cette arme gardera sa RoF 1 fois sur 2, à chaque fois que le dé coloré sera inférieur ou égal à 3.
Question 1: Si nous intégrons la RoF, quelle est la probabilité finale que l'unité cible reste non-impactée après épuisement de la RoF ?Commençons de manière empirique.
Au premier lancé de dé, l'unité aura 51% de chance de résister au tir. Donc au bout de 1 tir, la probabilité est de 51%.
1er Lancé de dés
51 % de No Impact
Mais sur ces 51% de No Impacts la moitié va se faire tirer une deuxième fois dessus
Donc à la fin du 1er lancé on a plutôt la situation suivante:
1er lancé de dés
51% de No Impact, dont la moitié (donc 25.5 %) aura épuisé la RoF de la HMG, et l'autre moitié (les autres 25.5%) se fera tirer dessus une deuxième fois
Soit 25.5% qui seront en No Impact de manière définitive et 25.5% qui risquent un Pin/Break/Partial Kill ou KIA
Lançons les dés une deuxième fois pour ceux du deuxième groupe. Ceux-ci ont encore 51% de chance de s'en tirer sans une égratignure.
Donc au bout du deuxième lancé, on a:
a) toujours ceux du premier lancé qui n'ont rien eu, et qui n'ont pas eu de deuxième tir = 25.5 %
b) ceux qui ont résisté deux fois aux tirs = 25.5% * 51% = 13 %
Ce qui fait donc une probabilité de 25.5+13=38.5 % de cible qui va résister en moyenne si on considère deux tirs
A partir de là, la situation devient itérative. Les 13% qui restent vont pour moitié subir un troisième tir, et l'autre moitié non. On aura donc au bout du troisième tir
a) toujours ceux du premier lancé qui n'ont rien eu, et qui n'ont pas eu de deuxième tir = 25.5 %
b) ceux qui ont résisté la 2ème aux tirs = 13 % /2 = 6.5 % et qui n'auront pas eu de troisième tir
c) et ceux qui auront résisté au 3ème tir, soit 6.5*51% = 3.3 %
Ce qui fait donc une probabilité de 25.5+6.5+ 3.3 =35.3 % de cible qui va résister en moyenne si on considère trois tirs
Est-ce que vous voyez le schéma apparaitre ????
Mathématiquement, la probabilité de résister à n tirs peut donc s'exprimer comme la somme de P/2 + (P/2)^2 + (P/2)^3 + .... + (P/2)^n-1 + 2 x (P/2)^n, où P est notre probabilité de No Impact (663 sur 1296)
Cette somme peut aussi s'écrire [1-(P/2)^n]/[1-(P/2)]. Comme 0<P<1, (P/2)^n va tendre vers zéro lorsque n tend vers l'infini.
Donc in fine, la somme tendra vers la valeur de 1/ (1-P/2)=34.37 %Question 2 :
est-ce le bon résultat ?
En fait, cela aurait été chouette, mais ce n'est pas le cas, à cause d'un truc tout con : le dé coloré qui sert à la ROF, influe aussi sur la probabilité Impact / No Impact du tir. C'est logique, un tir qui garde sa ROF a plus de chances de faire mal qu'un tir qui ne garde pas la ROF.
Reprenons les choses depuis le début (mais je préfère vous prévenir, on va monter d'un cran en complexité).
J'ai dit au début du post que la proba d'un No Impact était de 633 / 36^2. Cela reste vrai. Mais le truc, c'est que la répartition des Impact / No Impact ne se fait pas de manière homogène entre les tirs qui gardent et ceux qui perdent la ROF.
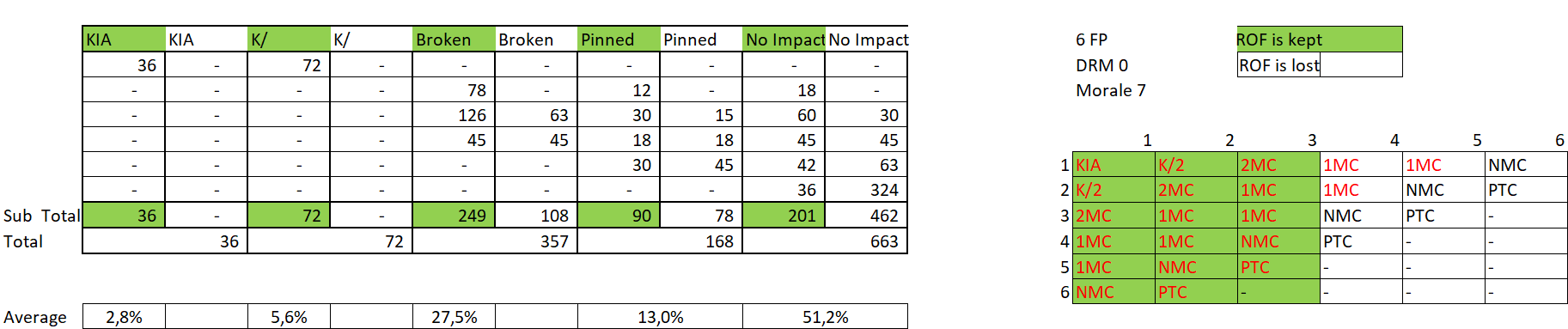
Sur le tableau ci-dessus j'ai mis en vert tous les résultats d'IFT qui correspondent à une ROF gardée. Il est clair qu'une ROF gardée signifie des résultats statistiquement plus graves d'une ROF perdue.
Si nous regardons, les cas de No Impact, nous voyons bien qu'ils représentent bien 663 cas sur 1296 au total. Sauf qu'ils se répartissent en 462 quand la ROF est perdue, et 201 quand la ROF est conservée.
Dit autrement la probabilité qu'une unité ne soit pas Pinned/Broken/Reduite ou KIA est 462/648 (la moitié de 1296) = 71 % quand la ROF est perdue et de 201/648=31 % quand la ROF est conservée.
Au bout de mon premier tir, il me faut maintenant considérer mes deux groupes de cibles : celles qui subiront un deuxième tir, et celle qui n'en subiront plus.
La première moitié aura eu 71 % de chances de résister au tir = 71% /2 = 35.5 %
La deuxième moitié aura eu 31 % de chance de résister au tir = 31 % / 2 = 15.5 %
Et si j'ajoute les deux, on a (71%+31%)/2 = 51 % - pas de différence pour le premier tir avec le cas précédent.
Pour le deuxième tir, les15.5 % de cibles heureuses vont de diviser en deux groupes : celles qui ne subiront pas de troisième tir - et celle-ci résisteront à 71%, et celles qui en subiront un troisième, qui elles ne résisteront qu'à 31 %
Donc au bout du deuxième tir, on aura:
La première moitié du premier tir qui aura eu 71 % de chances de résister au tir = 71% /2 = 35.5 %
La première moitié du deuxième tir qui aura eu 15.5/2% *71%= 5.5% de chance de résister au tir et qui n'en subira pas de 3ème
La deuxième moitié du deuxième tir qui aura eu 15.5/2% *31%= 2.4 % de chance de résister au tir et qui en subira pas un 3ème
Soit 35.5 + 5.5 +2.4 = 43.4 % de chances de résister au tir, pour deux tirs max.
Ici, la formule mathématique est un poil plus compliquée à sortir. Si on appelle P la probabilité de résister au tir quand la ROF est Perdue (donc 462/648) et C quand la ROF est conservée (201/648), la probabilité qu'un unité résiste à n tirs se calcule grâce à une suite:
Proba_1= 663/1296
Et Proba_n+1=0.5*(P+C*Proba_n)
Cette suite converge très vite, et au bout de 6 itérations on obtient la probabilité finale de 42,19%.Conclusion finaleLe fait que le dé coloré soit utilisé à la fois pour l'IFT et pour savoir la ROF est gardée a un effet sur la probabilité qu'une unité sorte pas Pinned/Broken/Réduite ou KIA du tir considéré. Si on suit les règles, l'unité cible s'en sortira sans égratignure dans 42.19% des cas. Je sais qu'il existe une variante où les tirs à ROF sont effectués avec un troisième dé qui ne sert qu'à cela. Dans cet autre cas, la probabilité que l'unité cible s'en sorte indemne serait plus faible (34.37 %). Et cela s'explique essentiellement par le différentiel sur le premier tir.
Dans les idées qui me traversent encore le crâne, je crois que je vais me laisser tenter par un autre challenge : reprendre cette histoire de ROF mais en y incluant tout un tas d'autres petites choses : quelles seraient les probabilités exactes qu'une unité de Morale 6, 7 ou 8 placée dans un bois résiste ou soit pinned, cassée, cassée avec perte ELR, Réduite, Réduite et cassée, Réduite et cassée avec perte ELR ou KIA si un MTR de 81 lui tirait dessus en tenant compte de son ROF de 3 et de son B12. Je ne suis pas encore sûr de savoir comment m'y prendre, mais le casse-tête promet d'être beau.
Sur ce il serait convenable que j'aille me coucher.
Salutations,
Patrice